Rozwiązanie zadania z zarządzania ryzykiem
ZADANIE
1. Należy policzyć prawdopodobieństwo zdania egzaminu, czyli udzielenia poprawnych odpowiedzi na minimum 18 poprawnych odpowiedzi z 20 pytań (odpowiedzi są: TAK/NIE).
Przy czym student posiada tylko połowę wiedzy z zakresu materiału wymaganego na egzaminie.
2A. Student douczy się jeszcze 20% materiału
2B. Egzaminujący obniży kryterium zdania egzaminu: minimum 15 poprawnych odpowiedzi z 20 pytań
2C. Jednocześnie student douczy się oraz egzaminujący obniży kryterium (2A i 2B jednocześnie)
ANALIZA WSTĘPNA
Jeżeli wiedzielibyśmy z góry, że na określone 10 pytań student zna odpowiedzi, to prawdopodobieństwo odpowiedzi na te pytania wynosiłoby 100%,
wtedy
zadanie sprowadziłoby się tylko do 10 pytań,
na które student nie zna odpowiedzi; prawdopodobieństwo prawidłowej odpowiedzi na każde z tych pytań wyniosłoby 50%.
Z treści zadania wynika, że nie można wcześniej przewidzieć na ile pytań student będzie znał odpowiedź.
Wiadomo tylko, że student zna połowę wiedzy z zakresu wymaganego materiału.
Oznacza to, że jeśli założymy, że: kule białe, to pytania, na które student zna odpowiedź, a kule czarne, to pytania, na które student nie zna odpowiedzi, to…
... nie należy sobie wyobrażać 20 kul (10 białych i 10 czarnych), ale nieskończoną liczbę kul białych i tyleż samo czarnych, z których wylosowanych zostanie 20 kul.
Po wstępnej analizie problemu należy zaplanować kolejne działania (podzielić problem na części).
PODZIAŁ PROBLEMU NA CZĘŚCI:
1. POLICZENIE PRAWDOPODOBNIEŃSTWA SUKCESU PRZY ZADANIU 1 PYTANIA
2. POLICZENIE PRAWDOPODOBNIEŃSTWA SUKCESU PRZY ZADANIU 2, 3 PYTAŃ (po to, aby zrozumieć schemat, którym powinniśmy się posługiwać)
3. POLICZENIE PRAWDOPODOBNIEŃSTWA SUKCESU DLA 20 PYTAŃ - ZGODNIE Z ZADANIEM (po wyciągnięciu wniosków z 2 PKT)
Podział problemu na części jest konieczny, dlatego aby:
- analiza napisanego planu postępowania pozwala na jego ocenę poprawności (zastanowienie się ponownie, po wcześniejszym jego opracowaniu)
- nie zgubić celu (w trakcie realizacji i po realizacji każdego z punktów można przypomnieć sobie punkty planu i miejsce realizacji)
- łatwiejszego zarządzania projektem, oceny po każdym zrealizowanym punkcie (zmiany kolejnych punktów planu w razie takiej potrzeby)

czyli prawdopodobieństwo udzielenia poprawnej odpowiedzi na zadane jedno, dowolne pytanie.
Problem policzenia prawdopodobieństwa udzielenia poprawnej odpowiedzi należy podzielić na dwa podproblemy:
1/ policzenie prawdopodobieństwa osiągnięcia sukcesu pod warunkiem, że student otrzyma pytanie, na które będzie znał odpowiedź (prawdopodobieństwo warunkowe) Jeżeli student dostanie takie pytanie (może je dostać z prawdopodobieństwem 50%), to odpowie poprawnie ze 100% prawdopodobieństwem (zob. Tablica 1).
2/ policzenie prawdopodobieństwa osiągnięcia sukcesu pod warunkiem, że student otrzyma pytanie, na które nie będzie znał odpowiedzi (prawdopodobieństwo warunkowe) Jeżeli student dostanie takie pytanie (może je dostać z prawdopodobieństwem 50%), to odpowie poprawnie z 50% prawdopodobieństwem (zob. Tablica 2).
Po połączeniu obydwu możliwości otrzymamy prawdopodobieństwo osiągnięcia sukcesu i porażki dla jednego pytania (zob. Tablica 3).
2A. POLICZENIE PRAWDOPODOBNIEŃSTWA SUKCESU PRZY ZADANIU 2 PYTAŃ
Przy dwóch pytaniach można wykorzystać wyliczone wcześniej prawdopodobieństwo osiągnięcia sukcesu dla jednego pytania.
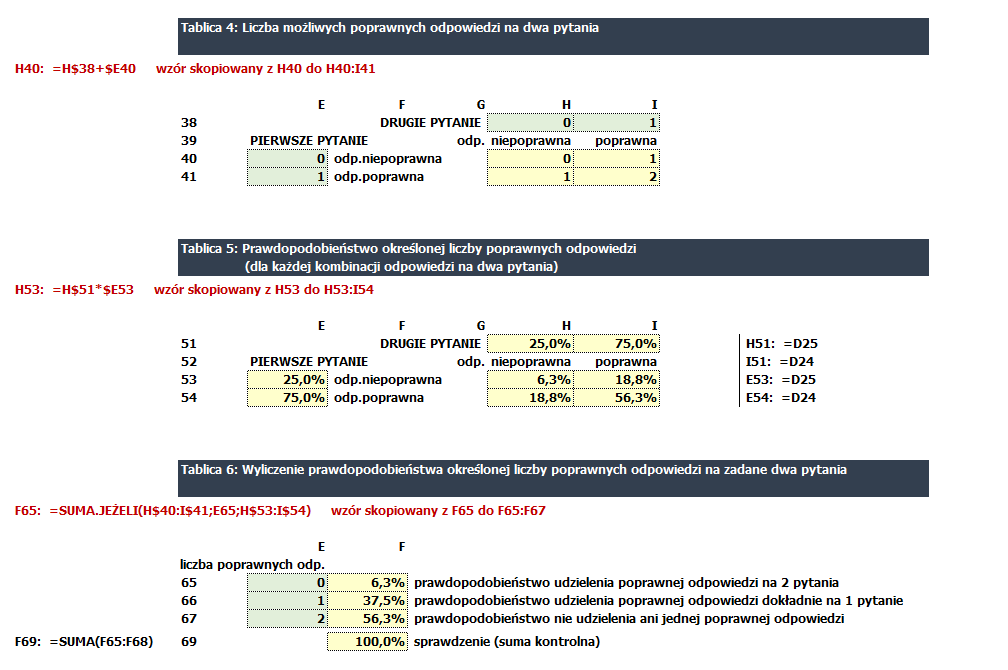
Należałoby tutaj zwrócić uwagę na fakt, że poprawnie można odpowiedzieć na dwa pytania, na jedno pytanie lub na zero pytań (zob. Tablice 4-6).
2B. POLICZENIE PRAWDOPODOBNIEŃSTWA SUKCESU PRZY ZADANIU 3 PYTAŃ
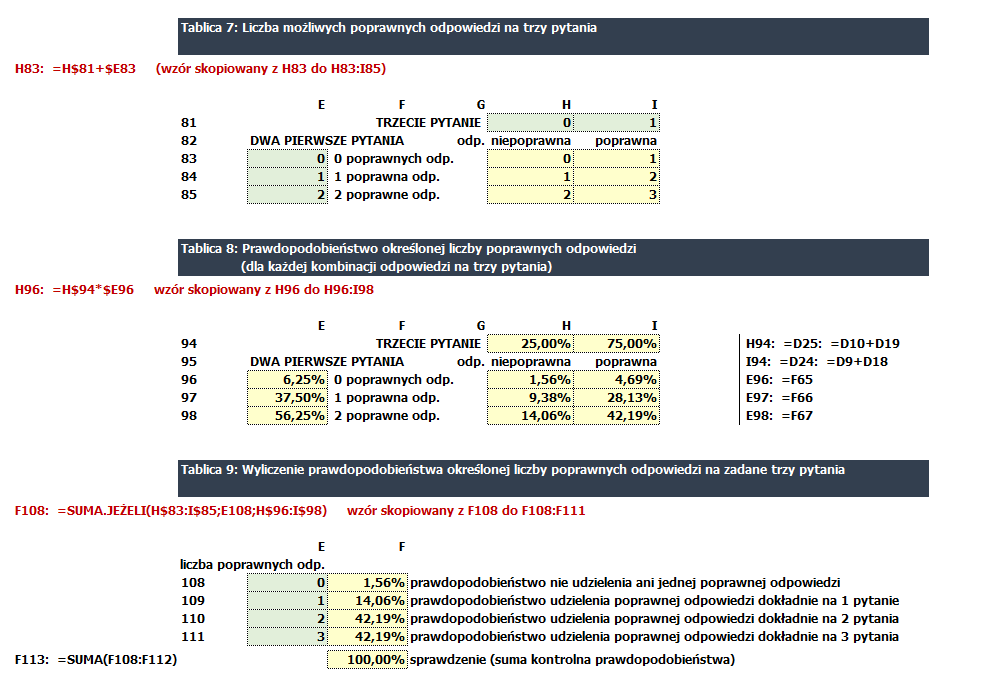
Przy trzech pytaniach można wykorzystać wyliczenie prawdopodobieństwo osiągnięcia sukcesu dla wyliczonych wcześniej: dwóch pytań i jednego pytania. Należałoby tutaj zwrócić uwagę na fakt, że poprawnie można odpowiedzieć na: trzy pytania, dwa pytania, jedno pytanie lub zero pytań (zob. Tablice 7-9).
Oczywiście, można sobie wyobrazić, że sposób kolejnych obliczeń można kontynuować, tylko, że pracochłonność w przypadku jego zastosowania jest duża.
Dlatego konieczne jest poszukanie narzędzi MS Excel, które pozwolą rozwiązać problem pracochłonności.
W MS Excel jest funkcja ROZKŁ.DWUM, która na podstawie liczby pytań (parametr 2), liczby poprawnych odpowiedzi (parametr 1) oraz prawdopodobieństwa (poprawnej jednej odpowiedzi - parametr 3) liczy to samo, co zostało policzone powyżej. Funkcja ta ma jeszcze parametr 4 (logiczny), który wskazuje, czy prawdopodobieństwo ma być liczone dla określonej liczby popranych odpowiedzi (FAŁSZ), czy narastająco (PRAWDA)
Wzór, po wpisaniu do komórki E145 został skopiowany do całego zakres komórek E145:G148.
Funkcja zewnętrzna JEŻELI.BŁĄD zamienia błędy na pusty ciąg znaków (zob. Tablice 10-11).

Uzyskane wyniki osiągnięte za pomocą funkcji ROZKŁ.DWUM są takie same jak w obliczeniach realizowanych krok po kroku.
Należy zauważyć, że w stosunku do zakładanego planu (zob. PODZIAŁ PROBLEMU NA CZĘSCI) konieczne było zmodyfikowanie go o WYSZUKANIE NARZĘDZIA W MS EXCEL DO REALIZACJI OBLICZEŃ
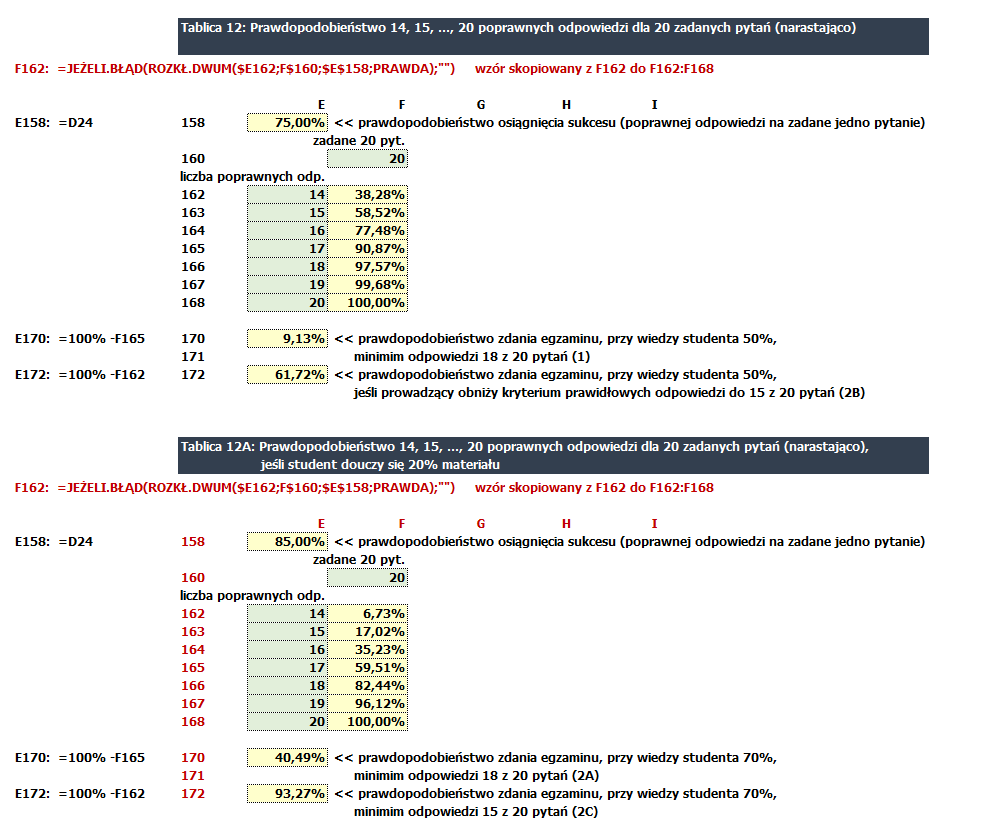
3. POLICZENIE PRAWDOPODOBNIEŃSTWA SUKCESU DLA 20 PYTAŃ - ZGODNIE Z ZADANIEM
Po przedstawieniu merytoryki problemu oraz narzędzia, którym można zadany problem rozwiązać, można zrealizować rozwiązanie zadania (zob. Tablice 12-12A).
Dla zadania: wyliczenia prawdopodobieństwa uzyskania minimum 18 odpowiedzi poprawnych z 20 pytań; przy 50% wiedzy studenta należy zsumować prawdopodobieństwo dla 18, 19 i 20.
Ze względu na fakt, że dla suma wszystkich prawdopodobieństw (dla: 0, 1, 2, …, 20) poprawnych odpowiedzi jest równa 100%, można zastosować wzór: 100% - suma prawdopodobieństw od 0 do 17.
Jeśli prawdopodobieństwo otrzymania pytania, na które student zna odpowiedź zmieni się z 50% do 70%, to prawdopodobieństwo osiągnięcia sukcesu (poprawnej odpowiedzi na zadane jedno pytanie) zwiększy się z 75% do 85%; wystarczy zmienić wartość w komórce D6 z 50% na 70%, a wynik (prawdopodobieństwo osiągnięcia sukcesu) zmieni się z 75% do 85% wtedy zmieni się również wynik w komórce E158 (Tablica 12A), oraz wyniki działania wzorów w 170 i 172 wierszu.